已知△ABC中，AB=AC，点D为直线BC上一动点（不与点B，C重合），以AD为边作△ADF（A，D，F按顺时针排列），使AD=AF，且∠BAC=∠DAF，连接CF．
（1）如图，当点D在边BC上时，求证：BC=CF＋CD．

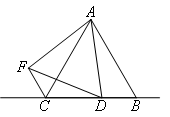
解题思路：（1）由∠BAC=∠DAF，得∠BAD=∠CAF；又因为AB=AC，AD=AF，因此根据三角形全等的判定定理           ，可以得到           ，由全等的性质得到                      ，通过等量代换可得BC=CF+CD．
①ASA；②SAS；③SSA；④△ADB≌△AFC；⑤△AFC≌△BAD；⑥△ADB≌△FCD；⑦BD=CF；
⑧BD=CF，BC=AC．
以上横线处依次所填正确的是(    )

（上接第1，2题）如图3，若以△ABC的边AB，AC为直角边向内作等腰直角三角形ABE和等腰直角三角形ACD，其他条件不变，结论DE=2AM依然成立，如图3-1，证明的方法是延长AM到F，
使MF=AM，连接BF．先证明△BFM≌CAM，再证明△ABF≌△EAD．证明△ABF≌△EAD时用到的三组条件是(    )

（上接第1题）如图2，当△ABC为一般三角形时，DE=2AM是否依然成立？若成立写出证明DE=2AM的思路；若不成立，说明理由．下列各项正确的是(    )

以△ABC的边AB，AC为直角边向外作等腰直角三角形ABE和等腰直角三角形ACD，
AB=AE，AC=AD，∠BAE=∠CAD=90°，M是BC中点，连接AM，DE．
（1）如图1，在△ABC中，当∠BAC=90°时，求AM与DE的数量关系．根据图1-1的辅助线，下面给出了解题的路线图：


①延长AM到F，使MF=AM，连接BF；②延长AM到F，使AM=MF；③延长AM到F，连接BF；
④BF=AC=AD，BF∥AC；⑤BM=CM；⑥AFB≌△EAD（ASA）；⑦ABF≌△EAD（SAS）．
以上横线处，依次所填正确的是(    )

（上接第4题）如图2所示，当直线与直线MA不垂直，且交点D，E在AB的异侧时，则线段AD，BE，AB之间的数量关系和证明思路正确的是(    )

如图1，直线AM∥BN，∠MAB与∠NBA的平分线交于点C，过点C作一条直线与两条直线MA，NB分别相交于点D，E．如图1所示，当直线与直线MA垂直时，求证：AB=AD+BE．下面给出了证明的路线图，如图1-1：


①△ADC≌△FEC；②△ADC≌△FBC；③AD=BF；④AD=EF；⑤∠1=∠3．
以上横线处，依次所填正确的是(    )

（上接第1，2题）如图3，在正五边形ABCDE中，在AB，BC边上分别取点M，N，使AM=BN，连接AN，EM交于点O，则∠EON=(    )

（上接第1题）如图2，在正方形ABCD中，在AB，BC边上分别取点M，N，使AM=BN，连接AN，DM交于点O，则∠DON的度数和解题思路正确的是(    )

七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果，内容如下：如图1，在等边三角形ABC中，在AB，AC边上分别取点M，N，使BM=AN，连接BN，CM交于点O，求∠NOC的度数．下面给出了解题的路线图，如图1-1：


①△NAB≌△MBC（SAS）；②△NAB≌△AMC（SSA）；③△AMC≌△NCB（SAS）；
④∠2=∠1；⑤BN=CM；⑥∠2=∠1，BN=CM．
以上横线处，依次所填正确的是(    )

（上接第4，5题）（3）在图1的基础上，将△BEF绕点B旋转，使点E在AB的延长线上，其他条件不变，如图3，为了证明EG和CG之间的数量和位置关系，类比（1），（2）中的辅助线和证明思路，需要作出的辅助线是(    )