已知：如图，在△ABC中，AD平分∠BAC交BC于点D，∠B=∠FDC，DE交AC于点F．
求证：∠AFE=2∠BAD．

证明：如图，
∵∠B=∠FDC（已知）
∴AB∥DF（同位角相等，两直线平行）
                                    
∵∠AFE是△ADF的一个外角（外角的定义）
∴∠AFE=∠ADF+∠DAF
       =2∠BAD（三角形的一个外角等于和它不相邻的两个内角的和）
横线处应填写的过程恰当的是(    )

已知：如图，AD与EB，FC分别相交于点G，H，∠E+∠F=180°．
求证：∠A+∠B+∠C+∠D=180°．

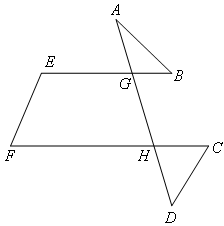
证明：如图，

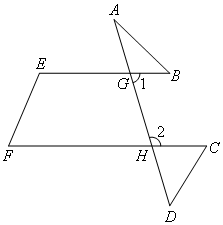
∵∠E+∠F=180°（已知）
∴BE∥CF（                       ）
∴∠1+∠2=180°（                       ）
∵∠1是△AGB的一个外角（外角的定义）
∴∠1=∠A+∠B（                       ）
∵∠2是△HDC的一个外角（外角的定义）
∴∠2=∠C+∠D（三角形的一个外角等于和它不相邻的两个内角的和）
∴∠A+∠B+∠C+∠D=∠1+∠2
                 =180°（等量代换）
①两直线平行，同旁内角互补；②同旁内角互补，两直线平行；③同旁内角互补；④三角形的一个外角等于和它不相邻的两个内角的和；⑤三角形的内角和是180°．
以上空缺处依次所填正确的是(    )

已知：如图，∠1与∠2互补．
求证：∠ADC=∠E+∠2．

证明：如图，
∵∠1+∠2=180°（已知）
∴AD∥BC（                       ）
∴∠2=∠EFD（                       ）
∵∠ADC是△EFD的一个外角（外角的定义）
∴∠ADC=∠E+∠EFD（                       ）
∴∠ADC=∠E+∠2（等量代换）
①两直线平行，同旁内角互补；②同旁内角互补，两直线平行；③两直线平行，同位角相等；④同位角相等，两直线平行；⑤三角形的一个外角等于和它不相邻的两个内角的和；⑥外角的定义．
以上空缺处依次所填正确的是(    )

已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，∠E=∠1.
求证：AD平分∠BAC.

证明：如图，

∵AD⊥BC，EG⊥BC（已知）
∴∠ADC=∠EGC=90°（垂直的性质）
∴EG∥AD（                    ）
∴∠E＝      （两直线平行，同位角相等）
∠1＝      （两直线平行，内错角相等）
∵∠E=∠1（已知）
∴∠2＝∠3（等量代换）
∴AD平分∠BAC（角平分线的定义）
①内错角相等，两直线平行；②同位角相等，两直线平行；③两直线平行，同位角相等；
④∠2；⑤∠3．
以上空缺处依次所填正确的是(    )

已知：如图，AB∥CD，∠A=∠D．试说明AC∥DE成立的理由．
下面是彬彬同学进行的推理，请你将彬彬同学的推理过程补充完整．

证明：如图，
∵AB∥CD（已知）
∴∠A=      （两直线平行，内错角相等）
∵∠A=∠D（已知）
∴∠ACD=∠D（                  ）
∴AC∥DE（                  ）
①∠ACD；②∠D；③等式的性质；④等量代换；⑤两直线平行，内错角相等；
⑥内错角相等，两直线平行．
以上空缺处依次所填正确的是(    )