已知:如图,在四边形ABCD中,AB=BC=CD=AD,BD平分∠ABC,E为BD上任意一点,连接AE,CE.
求证:△ADE≌△CDE.
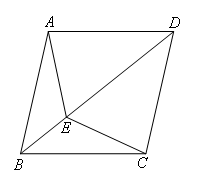
证明:如图,
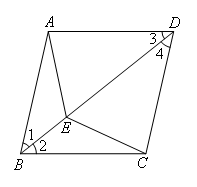
∵BD平分∠ABC
∴∠1=∠2
∵AB=BC=CD=AD
∴
∴∠3=∠4
在△ADE与△CDE中
∴△ADE≌△CDE( )
请你仔细观察下列序号所代表的内容:
①∠1=∠3,∠2=∠4;②AE=CE;③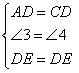 ;④
;④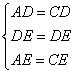 ;⑤SSS;
;⑤SSS;
⑥SAS;⑦SSA
以上空缺处依次所填最恰当的是( )
- A.②④⑤
- B.①③⑦
- C.①③⑥
- D.②③⑥
答案
正确答案:C
要证△ADE≌△CDE,需要找三组条件,
已知AD=CD,DE是公共边,
要证全等,还需要找一组边对应相等或者这两边的夹角相等;
由题中条件BD平分∠ABC,得到∠1=∠2,
又因为AB=AD,BC=CD,根据等边对等角可知∠1=∠3,∠2=∠4,
所以∠3=∠4.
至此,证全等的三组条件都已找到,
利用SAS可证得△ADE≌△CDE.
因此空缺处依次填最恰当的是①③⑥.
故选C.
略









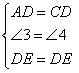 ;④
;④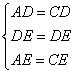 ;⑤SSS;
;⑤SSS;