Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=4，BC=3，则BD的值为（）

如图，在平面直角坐标系中，点A（0，6），点B是x轴上的一个动点，连结AB，取AB的中点M，将线段MB绕着点B按顺时针方向旋转90°，得到线段BC．过点B作x轴的垂线交直线AC于点D．设点B坐标是（t，0）．（1）当t ＝4时，求直线AB的解析式；（2）当t＞0时，用含t的代数式表示点C的坐标及△ABC的面积；（3）是否存在点B，使△ABD为等腰三角形？若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由．

如图1，抛物线y=ax²+bx+3经过点A（-3，0），B（-1，0）两点，（1）求抛物线的解析式；（2）设抛物线的顶点为M，直线y=-2x+9与y轴交于点C，与直线OM交于点D，现将抛物线平移，保持顶点在直线OD上，若平移的抛物线与射线CD（含端点C）只有一个公共点，求它的顶点横坐标的值或取值范围；（3）如图2，将抛物线平移，当顶点至原点时，过Q（0，3）作不平行于x轴的直线交抛物线于E、F两点，问在y轴的负半轴上是否存在一点P，使△PEF的内心在y轴上，若存在，求出点P的坐标；若不存在，说明理由．

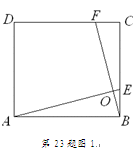
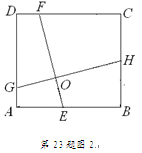
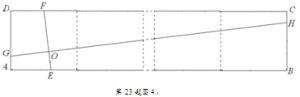
(2010年浙江绍兴市)（1）如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.（2）如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH＝90°,EF＝4.求GH的长.（3）已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,∠FOH＝90°,EF＝4.直接写出下列两题的答案：①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连接OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连接CF．（1）当∠AOB=30°时，求弧AB的长度；（2）当DE=8时，求线段EF的长；（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此时点E的坐标；若不存在，请说明理由．

如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：①CE=BD；②△ADC是等腰直角三角形；③∠ADB=∠AEB；④CD•AE=EF•CG；一定正确的结论有（　　　　）

(1)情境观察:将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示.将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A(A′)、B在同一条直线上，如图2所示．观察图2可知：与BC相等的线段是_____，∠CAC′=______°．
(2)问题探究:如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q.试探究EP与FQ之间的数量关系，并证明你的结论.
(3)拓展延伸:如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF，射线GA交EF于点H.若AB=k AE，AC=k AF，试探究HE与HF之间的数量关系，并说明理由.

已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K．过D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H．
（1）求证：AE=CK；
（2）如果AB=a，AD=     (a为大于零的常数)，求BK的值．
（3）若F是EG的中点，且DE=6，求⊙O的半径和GH的长．

(2011江苏)如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8 cm，P为BC的中点．动点Q从点P出发，沿射线PC方向以2 cm /s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为ts．

（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；
（2）已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．

（2011山东）已知AC⊥BC于C，BC=a，CA=b，AB=c，下列选项中的半径为的是（     ）