已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(3)如图3,当点D在边CB的延长线上且点A、F分别在直线BC的异侧时,其他条件不变,∠AFC、∠ACB、∠DAC之间的等量关系为()

已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(2)如图2,当点D在边BC的延长线上时,其他条件不变,∠AFC、∠ACB、∠DAC之间的等量关系为()

已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,下列结论:①∠ADB=∠AFC;②∠AFC=∠ACB+∠DAC.正确的是()

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(3)如图3,若点E是线段AC延长线上的任意一点,其它条件不变.求证:BE=EF.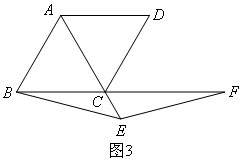

参考小宇同学的作法,第一步应为           ③             .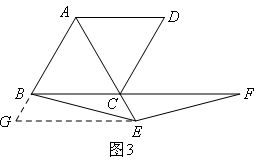

接下来的证明过程如下:∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴        ④         ,
∴BE=EF.
③,④处横线上所填内容分别是()

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(2)若点E是线段AC上的任意一点,其它条件不变.如图2,判断线段BE、EF有怎样的数量关系并证明.小宇同学展示出如下正确的作法: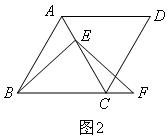
解:BE=EF,证明如下:如图2,        ①        ,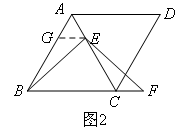

∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=120°,
∴        ②         ,
∴BE=EF;
①,②处横线上所填内容分别是()

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(1)若点E是线段AC的中点,如图1,则BE与EF的数量关系为BE       EF;

已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间的数量关系为()

已知：正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.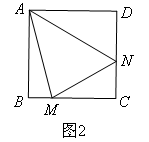小明猜测线段BM,DN和MN之间的数量关系为BM+DN=MN.理由如下:
如图,            ①             .

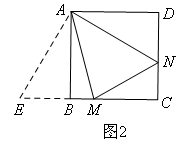
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=∠ABE =90°,
∴△ABE≌△ADN,
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=45°,
又∵AM=AM,
∴        ②         ,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN.
①,②处横线上所填内容分别是()

已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(1)当∠MAN绕点A旋转到BM=DN时(如图1),线段BM、DN、MN之间的数量关系为()