如图，在△ABC中，∠ABC=45°，CD⊥AB于D，BE平分∠ABC，
且BE⊥AC于E，与CD相交于点F，DH⊥BC于H，交BE于G．下列结论：
①BD=CD；②AD+CF=BD；③AE=CE；④AE=BG．其中正确的结论是(    )

如图，在△ABC中，∠BAC=45°，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，且EH=EB，小彤在研究时得到四个结论：①∠ABC=45°；②△AEH≌△CEB；③AE-BE=CH；④△AEC是等腰直角三角形．其中正确的结论是(    )

如图，△ABC是等边三角形，AB=BC=AC，∠ABC=∠ACB=60°，
∠EDF=60°，BD=CD，∠DBC=∠DCB=30°，∠BDC=120°，延长AC到点G，使CG=BE．
则下列结论：①△EBD≌△GCD；②△EFD≌△GFD；③EF=BE+CF；④△FDG是等边三角形．其中正确的结论是(    )

如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF，CE．下列结论：①△BDF≌△CDE；②CE=BF；③BF∥CE；④．其中正确的结论是(    )

已知：如图，在四边形ABCD中，AD=AB，∠D=∠ABC=∠DAB=90°，E，F分别为CD，BC边上的点，且∠EAF=45°，延长CB到点G，使BG=DE，连接EF，AG．
求证：EF=DE+BF．

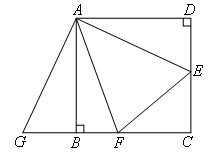
证明：如图，

                           
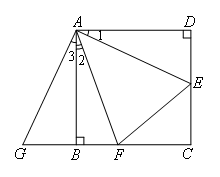
在△ADE和△ABG中

∴△ADE≌△ABG（SAS）
∴                            
∵∠DAB=90°，∠EAF=45°
                            
即∠FAE=∠FAG
在△FAE和△FAG中
                           
∴△FAE≌△FAG（SAS）
∴EF=GF
∵DE=BG
∴EF=BG+BF
    =DE+BF
请你仔细观察下列序号所代表的内容：
①；②∵∠D=∠ABG=90°；③；

④∠1=∠3，∠G=∠AED；⑤∠1=∠3，AE=AG；⑥；⑦；

⑧；⑨．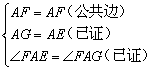
以上空缺处依次所填最恰当的是(    )

已知：如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且BD=CD．
求证：Rt△DEB≌Rt△DFC．

证明：如图，

                            
∵DE⊥AB，DF⊥AC
∴∠DEA=∠DFA=∠DFC=90°
在△ADE和△ADF中

∴                            
∴                            
在Rt△DEB和Rt△DFC中
                            
①∵∠1=∠2；②；③△ADE≌△FDA（ASA）；④△ADE≌△ADF（AAS）；
⑤DE=DF；⑥∠EDB=∠FDC；⑦；⑧．
以上空缺处依次所填最恰当的是(    )

如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上的点E处测得
∠AEP=74°，∠BEQ=30°，在点F处测得∠AFP=60°，∠BFQ=60°，EF=1km．
（1）AB与AE之间的数量关系为(    )

已知：如图，点B，E，F，C在同一直线上，AB=DC，BE=CF，∠B=∠C．
求证：OA=OD．

证明：如图，过O作OG⊥EF于G．

∵BE=CF
∴BE+EF=CF+EF
即BF=CE
在△ABF和△DCE中
                        
∴△ABF≌△DCE（     ）
∴∠2=∠1，AF=DE
∵OG⊥EF
∴∠OGE=∠OGF=90°
在△OEG和△OFG中
                        
∴△OEG≌△OFG（     ）
∴OE=OF（全等三角形对应边相等）
∴AF-OF=DE-OE
即OA=OD
请你仔细观察下列序号所代表的内容：
①；②；③SAS；④SSA；⑤ASA；
⑥AAS；⑦；⑧．
以上空缺处依次所填正确的是(    )

已知：如图，在四边形ABCD中，AD=BC，AB=CD，E，F分别为AD，CB
延长线上一点，且DE=BF．
求证：∠E=∠F．

证明：如图，连接BD，

在△ADB和△CBD中

∴                    （SSS）
∴                        
∵∠ADB+∠EDB=180°
  ∠CBD+∠FBD=180°
∴∠EDB=∠FBD
在△EDB和△FBD中
                        
∴△EDB≌△FBD（     ）
∴∠E=∠F
请你仔细观察下列序号所代表的内容：
①△ADB≌△CBD；②△CBD≌△ABD；③∠ADB=∠CBD；④∠A=∠C；
⑤；⑥；⑦SSA；⑧SAS．
以上空缺处依次所填正确的是(    )

已知：如图，在四边形ABCD中，AD∥BC，AD=BC．
求证：∠A=∠C．

证明：如图，连接BD，

                         
在△ABD和△CDB中
                         
∴△ABD和△CDB（     ）
∴∠A=∠C
请你仔细观察下列序号所代表的内容：
①；②；③；④；
⑤SAS；⑥SSA．
以上空缺处依次所填正确的是(    )