1编号:139065题型:解答题测试正确率:0%
探索新知:
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示)
深入研究:
(3)如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.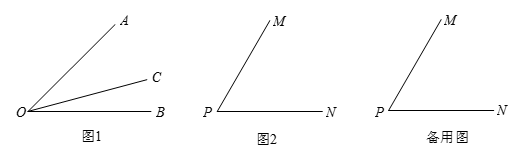
2编号:139043题型:解答题测试正确率:0%
背景知识:数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a,b,则A,B两点之间的距离AB=|a-b|,线段AB的中点表示的数为![]() .
.
问题情境:如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
综合运用:
(1)填空:①A,B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,P,Q两点相遇,并写出相遇点所表示的数.
(3)求当t为何值时,PQ=![]() AB.
AB.
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
3编号:139041题型:解答题测试正确率:0%
定义:对于一个两位数x,如果x满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“相异数”,将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数,将这个新两位数与原两位数的求和,同除以11所得的商记为S(x).如a=13的个位数字与十位数字对调后的新两位数为31,新两位数与原两位数的和为13+31=44,和44除以11的商为44÷11=4,所以S(13)=4.
(1)计算:S(43)= .
(2)若一个“相异数”y的十位数字是k,个位数字是2(k-1),且S(y)=10,求相异数y.
(3)小慧同学发现若S(x)=5,则“相异数”x的个位数字与十位数字之和一定为5,请判断小慧的发现是否正确?如果正确,说明理由;如果不正确,举出反例.
6编号:138347题型:解答题测试正确率:0%
10编号:138280题型:解答题测试正确率:0%