1编号:139524题型:解答题测试正确率:0%
2编号:139205题型:解答题测试正确率:0%
(2021武汉)问题提出
如图1,在△ABC和△DEC中,∠ACB=∠DCE=90°,BC=AC,EC=DC,点E在△ABC内部,直线AD与BE交于点F.线段AF,BF,CF之间存在怎样的数量关系?
问题探究
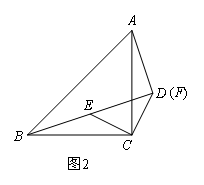
(1)先将问题特殊化如图2,当点D,F重合时,直接写出一个等式,表示AF,BF,CF之间的数量关系;
(2)再探究一般情形如图1,当点D,F不重合时,证明1中的结论仍然成立.
问题拓展
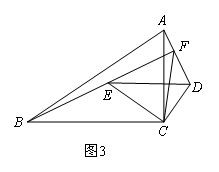
如图3,在△ABC和△DEC中,∠ACB=∠DCE=90°,BC=kAC,EC=kDC(k是常数),点E在△ABC内部,直线AD与BE交于点F.直接写出一个等式,表示线段AF,BF,CF之间的数量关系.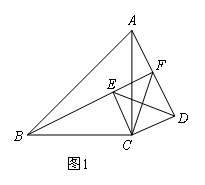
3编号:136996题型:解答题测试正确率:0%
(1)操作发现
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′,
连接BB′;
②在①中所画图形中,∠AB′B= °.
(2)问题解决
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到
AE,连接DE,求∠ADE的度数.
(3)拓展延伸
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).


4编号:136993题型:解答题测试正确率:0%
5编号:136972题型:解答题测试正确率:0%
如图,在矩形ABCD中,AB=9,AD=12.动点E从点B出发,沿线段BC(不包括端点B,C)以每秒2个单位长度的速度,匀速向点C运动;动点F从点C出发,沿线段CD(不包括端点C,D)以每秒1个单位长度的速度,匀速向点D运动;点E,F同时出发,同时停止.连接AF并延长交BC的延长线于点M,再把AM沿AD翻折交CD的延长线于点N,连接MN.设运动时间为t秒.
(1)当t为何值时,△ABE∽△ECF;
(2)在点E运动的过程中是否存在某个时刻使AE⊥AN?若存在,请求出t的值;若不存在,请说明理由;
(3)在运动的过程中,△AMN的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.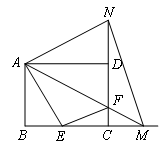
6编号:136945题型:解答题测试正确率:0%
7编号:136929题型:解答题测试正确率:0%
8编号:136928题型:解答题测试正确率:0%
9编号:136879题型:解答题测试正确率:0%
10编号:136754题型:解答题测试正确率:0%