如图，在正方形ABCD中，∠ABC=∠BCD=90°，AB=BC=CD=AD．E为BC边上一点，
且AE=DE，AE与对角线BD交于点F，∠ABF=∠CBF，连接CF，交ED于点G．求证：DE⊥CF．

证明：如图，

在Rt△ABE和Rt△DCE中

∴Rt△ABE≌Rt△DCE（HL）
∴                 
在△ABF与△CBF中
                 
∴               
∴               
∴∠2=∠3
∵∠3+∠4=90°
∴∠2+∠4=90°
∴∠DGC=90°
∴DE⊥CF
请你仔细观察下列序号所代表的内容：
①∠1=∠2（全等三角形对应角相等）；②∠1=∠3（全等三角形对应角相等）；
③∠ABE=∠DEC（全等三角形对应角相等）；
④；⑤；
⑥△ABF≌△CBF（SAS）；⑦△ABF≌△CBF（SSS）；
⑧∠AFB=∠CFB（全等三角形对应角相等）．
以上空缺处依次所填正确的是(    )

已知：如图，点A，C在直线EF上，BC=AD，AB=CD，AE=CF，求证：∠E=∠F．

证明：如图，
在△ABC和△CDA中
                    
∴                  
∴∠ACB=∠CAD（全等三角形对应角相等）
∵AE=CF
∴AE+AC=CF+AC
即EC=FA
在△ECB和△FAD中
                           
∴                         
∴∠E=∠F（全等三角形对应角相等）
请你仔细观察下列序号所代表的内容：
①；②；
③；④；
⑤△ABC≌△CDA（SSS）；⑥△ABC≌△CDA（SAS）；
⑦△ECB≌△FAD（SAS）；⑧△EAB≌△FCD（SAS）．
以上空缺处依次所填正确的是(    )

已知：如图，∠E=∠D，AM=CN，ME=ND．求证：△ABE≌△CBD．

证明：如图，
在△BME和△BND中

∴△BME≌△BND（AAS）
∴                  
∵AM=CN，ME=ND
∴AM+ME=CN+ND
即AE=CD
在△ABE和△CBD中
                         
∴△ABE≌△CBD（      ）
请你仔细观察下列序号所代表的内容：
①BE=BD（全等三角形对应边相等）；②∠BME=∠BND（全等三角形对应角相等）；
③BM=BN（全等三角形对应边相等）；④；
⑤；⑥；⑦SAS；⑧AAS．
以上空缺处依次所填正确的是(    )

已知:如图，AB=EF，BC=FG，AC=EG，D为BC中点，H为FG中点，求证：AD=EH．

证明：如图，
在△ABC与△EFG中

∴                  
∴                  
∵D为BC中点，H为FG中点

∵BC=FG
∴BD=FH
在△ABD与△EFH中
                      
∴△ABD≌△EFH（     ）
∴AD=EH．
①；②；③；
④∠BAD=∠FEH（全等三角形对应角相等）；⑤∠B=∠F（全等三角形对应角相等）；
⑥SSS；⑦SAS；⑧△ABC≌△FEG（SSS）；⑨△ABC≌△EFG（SSS）．
以上空缺处依次所填正确的是(    )

已知：如图，AB=AC，DB=DC，F是AD的延长线上的一点．求证：△ABF≌△ACF．

证明：如图，
在△ADB和△ADC中
                      
∴△ADB≌△ADC（      ）
∴                      
在△ABF和△ACF中
                    
∴△ABF≌△ACF（      ）
请你仔细观察下列序号所代表的内容：
①；②；
③SSS；④SAS；⑤SSA；⑥∠ABD=∠ACD（全等三角形对应角相等）；
⑦∠BAD=∠CAD（全等三角形对应角相等）；
⑧；⑨．
以上空缺处依次所填正确的是(    )

已知:如图,AB=EF,BC=FG,AD=EH,D为BC的中点,
H为FG的中点.求证:△ABC≌△EFG.

证明:
∵D为BC的中点,H为FG的中点
∴,
∵BC=FG
∴BD=FH
在△ABD与△EFH中
                      
∴                    
∴                    
在△ABC与△EFG中
                    
∴                  
请你仔细观察下列序号所代表的内容:

以上空缺处依次填写正确的选项是(    )

已知:如图,∠C=∠D,AD=BC,CE=DF.求证:AO=BO.

证明:如图,
∵CE=DF
∴CE+EF=DF+EF
即CF=DE
在△AED和△BFC中
                    
∴                  
∴AE=BF(全等三角形对应边相等)
∠AED=∠BFC(全等三角形对应角相等)
在△AEO和△BFO中
                           
∴                         
∴AO=BO(全等三角形对应边相等)

请你仔细观察下列序号所代表的内容:
①,②,③,
④,⑤△AED≌△BFC(SAS),⑥△ADE≌△BFC(SAS),⑦△AEO≌△BFO(AAS),
⑧△AEO≌△BFO(SAS),以上空缺处依次填写正确的是(    )

已知点A,C在直线EF上,AD=BC,AB=DC,AE=CF,求证:=∠F

证明:如图,
在△ABC和△CDA中
                    
∴                  
∴∠ACB=∠CAD(全等三角形对应角相等)
∵AE=CF
∴AE+AC=CF+AC
即EC=AF
在△ECB和△FAD中
                           
∴                         
∴=∠F(全等三角形对应角相等)
请你仔细观察下列序号所代表的内容:
①,②,③,
④,⑤△ABC≌△CDA(SSS),⑥△ABC≌△CDA(SAS),⑦△ECB≌△FAD(SAS),
⑧△EAB≌△FCD(SAS),以上空缺处依次填写正确的是(    )

已知:如图,在△ABC中,点D是BC的中点,DF⊥AB,DE⊥AC,垂足分别是F,E,DF=DE,试猜想
AB和AC的数量关系,并证明你的猜想.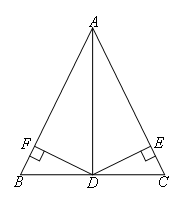

解:AB=AC,理由如下,
∵点D是BC的中点
∴           
∵DF⊥AB,DE⊥AC
∴∠BFD=∠AFD=∠AED=∠CED=90°
在Rt△BDF和Rt△CDE中
           
∴Rt△BDF≌Rt△CDE           
∴BF=CE(全等三角形对应边相等)
在Rt△AFD和Rt△AED中
           
∴Rt△AFD≌Rt△AED           
∴AF=AE(全等三角形对应边相等)
∴BF+AF=CE+AE
即AB=AC
请你仔细观察下列序号所代表的内容:
①,②BD=CD,③,④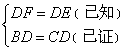,⑤SAS,⑥HL,
⑦,⑧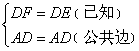,以上空缺处依次填写正确的是(    )

已知:如图,∠D=∠E,AM=ME=CN=DN.
试猜想AB和BC的数量关系,并证明你的猜想.

解:∴AB=BC,理由如下:
在△BME和△BND中
                 
∴△BME≌△BND           
∴                  (全等三角形对应边相等)
∵AM=ME=CN=DN
∴AM+ME=DN+CN
即AE=CD
在△ABE和△CBD中
                 
∴△ABE≌△CBD           
∴AB=BC(全等三角形对应边相等)
请你仔细观察下列序号所代表的内容:
①,②,③ASA,④AAS,⑤SAS,⑥BE=BD,
⑦∠BME=∠BND,⑧,⑨,以上空缺处依次填写正确的是(    )