如图,在等边△ABC中,D为BC边上的一点,P为AC边上的一点,∠ADP=60°,BD=1,CP=,则△ABC的边长为()

如图,在等腰Rt△ABC中,AC=BC,以斜边AB为一边作等边△ABD,使点C,D在AB的同侧;再以CD为一边作等边△CDE,使点C,E落在AD的异侧.若AE=1,则CD的长为()

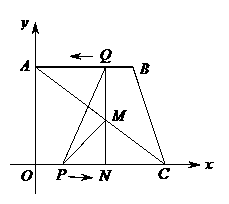
如图，直角梯形OABC中，AB∥OC，∠OAB=90°且OA=AB，点A、C的坐标分别为（0,3）、（4,0），动点P从O点出发，沿线段OC向点C作匀速运动；动点Q从点B出发，沿线段BA向点A作匀速运动．过Q点垂直于AB的射线交AC于点M，交OC于点N．P、Q两点同时出发，速度都为每秒1个单位长度．当Q点运动到A点，P、Q两点同时停止运动．设点Q运动的时间为t秒．
（1）求NC，MC的长（用含t的代数式表示）；
（2）当t为何值时，四边形PCBQ构成平行四边形？
（3）是否存在某一时刻，使射线QN恰好将△AOC的面积和周长同时平分？若存在，求出此时t的值；若不存在，请说明理由；
（4）探究：t为何值时，△PMC为等腰三角形．

如图，AA′=BB′=CC′=2,∠AOB′=∠BOC′=60°，则的大小关系是( )

（2011河北）如图1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置，得到图2，则阴影部分的周长为()．

（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连接ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE．（下面请你完成余下的证明过程）
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：当∠AMN=           时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

（2009年·烟台中考）如图，等边△ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，则CD的长为（）

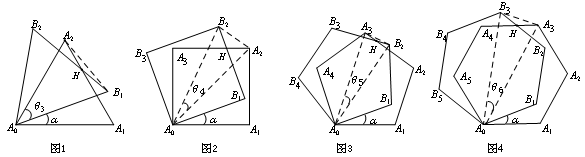
（2010江西）课题：两个重叠的正多边型，其中一个绕某一顶点旋转所形成的有关问题。实验与论证设旋转角∠A₁A₀B₁=α（α1A₀A₂）,θ₃，θ₄，θ₅，θ₆，所表示的角如图所示。
（1）用含α的式子表示角的度数：θ₃=　　　　　　　　　　_θ₄=　　　　　　　　　　　θ₅=_________
　　　　　　　　
（2）图1－图4中，连接A₀H时，在不添加其他辅助线的情况下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请选择期中的一个图给出证明；若不存在，请说明理由；归纳与猜想设正n边形A₀A₁A₂…A_n－1与正n边形A₀B₁B₂…B_n－1重合（其中，A₁与B₁重合），现将正n边形A₀B₁B₂…B_n－1绕顶点A₀逆时针旋转α（）．
（3）设θ_n与上述“θ₃，θ₄，…”的意义一样，请直接写出θ_n的度数；（4）试猜想在正n边形的情形下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请将这条线段用相应的顶点字母表示出来（不要求证明）；若不存在，请说明理由．

如图所示，以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF，猜想：四边形ADEF是什么四边形，试证明你的结论．