1编号:138102题型:解答题测试正确率:0%
(2020鄂尔多斯)我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x-h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x-a)2+(y-b)2=r2,如:圆心为点P(-2,1),半径为3的圆的方程为(x+2)2+(y-1)2=9.
(1)以点M(-3,-1)为圆心,![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)如图,以点B(-3,0)为圆心的圆与y轴相切于原点,点C是⊙B上一点,连接OC,作BD⊥OC,垂足为点D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,求证:EC是⊙B的切线;
②在BE上是否存在一点Q,使QB=QC=QE=QO?若存在,求点Q的坐标,并写出以点Q为圆心,以QB为半径的⊙Q的方程;若不存在,请说明理由.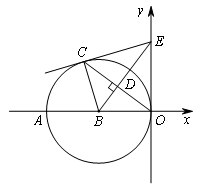
2编号:135457题型:解答题测试正确率:0%
3编号:135433题型:解答题测试正确率:0%
4编号:134712题型:解答题测试正确率:0%
5编号:123647题型:解答题测试正确率:0%
定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
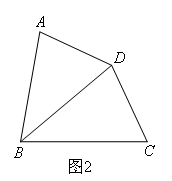
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;
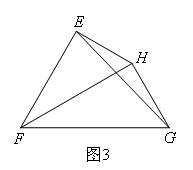
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为![]() ,求FH的长.
,求FH的长.