2编号:110363题型:单选题测试正确率:0%
3编号:110142题型:单选题测试正确率:0%
已知:如图,CE平分∠ACD,点F是CA延长线上的一点,FG∥EC交AB于点G.
若∠1=60°,∠B=40°,求∠2的度数.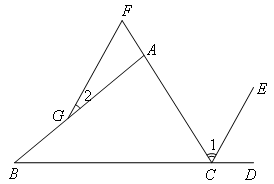
解:如图,
∵FG∥CE(已知)
∴∠F=∠1(两直线平行,内错角相等)
∵∠1=60°(已知)
∴∠F=60°(等量代换)
∴∠BAC=∠ACD-∠B=120°-40°=80°(等式性质)∵∠BAC是△FGA的一个外角(外角的定义)
∵∠BAC=∠2+∠F(三角形的一个外角等于和它不相邻的两个内角的和)
∴∠2=∠BAC-∠F=80°-60°=20°(等式性质)
横线处应填写的过程,顺序正确的是( )
①∵CE平分∠ACD(已知)
②∵∠ACD是△ABC的一个外角(外角的定义)
③∵∠B=40°(已知)
④∴∠ACD=2∠1=2×60°=120°(角平分线的定义)
⑤∴∠ACD=∠B+∠BAC(三角形的一个外角等于和它不相邻的两个内角的和)
⑥∴∠DCE=∠1=60°(角平分线的定义)
⑦∵∠ACE是△ABC的一个外角(外角的定义)
9编号:108921题型:单选题测试正确率:0%
10编号:108867题型:单选题测试正确率:0%
请根据过程示范,完成下题.
例题:已知:如图,D是△ABC的边AC上一点,∠A=60°,∠ABD=20°,求∠BDC的度数.
过程示范如下:
解:如图,
∵∠BDC是△ABD的一个外角(外角的定义)
∴∠BDC=∠A+∠ABD(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠A=60°,∠ABD=20°(已知)
∴∠BDC=60°+20°=80°(等量代换)
问题:
已知:如图,AB与CD相交于点E,点C,B,F在同一条直线上,∠1=70°,∠C=45°,求∠EBF的度数.
解:如图,
∵∠1=70°(已知)
∴∠CEB=∠1=70°(对顶角相等)
①∵∠EBF是△ECB的一个外角(外角的定义)
②∵∠EBF=∠C+∠CEB(外角的定义)
③∵∠C=45°(已知)
④∴∠EBF=∠C+∠CEB(三角形的一个外角等于和它不相邻的两个内角的和)
⑤∴∠EBF=45°+70°=115°(等量代换)
横线处应填写的过程,顺序正确的是( )