如图，直线y=-3x+3与x轴，y轴分别交于点A，B，抛物线y=a(x-2)²+k经过点A，B，并与x轴交于另一点C，其顶点为P．
（1）求a，k的值；
（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q的坐标；
（3）在抛物线及其对称轴上分别取点M，N，使A，C，M，N为顶点的四边形为正方形，求此正方形的边长．

如图1，抛物线y=ax²+bx+c经过点A(-4，0)，B(1，0)，C(0，3)，点P在抛物线
y=ax²+bx+c上，且在x轴的上方，点P的横坐标记为t．
（1）求抛物线的解析式；
（2）如图2，过点P作y轴的平行线交直线AC于点M，交x轴于点N，若MC平分∠PMO，求t的值；
（2）点D在直线AC上，点E在y轴上，且位于点C的上方，那么在抛物线上是否存在点P，使得以点C，D，E，P为顶点的四边形是菱形？若存在，请直接写出菱形的面积．

如图，抛物线y=ax²+bx-2的对称轴是直线x=1，与x轴交于A，B两点，与y轴交于点C，点A的坐标为(-2，0)，点P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E．
（1）求抛物线解析式．
（2）若点P在第一象限内，当OD=4PE时，求四边形POBE的面积．
（3）在（2）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．

如果一条抛物线y=ax²+bx+c（a≠0）与x轴有两个交点，那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，[a，b，c]称为“抛物线系数”．
（1）任意抛物线都有“抛物线三角形”是       （填“真”或“假”）命题；
（2）若一条抛物线系数为[1，0，-2]，则其“抛物线三角形”的面积为          ；
（3）若一条抛物线系数为[-1，2b，0]，其“抛物线三角形”是个直角三角形，求该抛物线的解析式；
（4）在（3）的前提下，该抛物线的顶点为A，与x轴交于O，B两点，点P在抛物线上，过点P作PQ⊥x轴于点Q．若△PQB∽△OAB，请直接写出此时点P的坐标．

如图，在平面直角坐标系中，抛物线与x轴交于A，B两点，与y轴交于点C，点A的坐标为(-1，0)，点C的坐标为(0，-2)，已知点E(m，0)是线段AB上的动点（点E不与点A，B重合），过点E作PE⊥x轴交抛物线于点P，交BC于点F．
（1）求该抛物线的解析式．
（2）当时，请求出m的值．
（3）是否存在这样的m值，使得△BEP与△ABC相似？若存在，直接写出此时m的值；若不存在，请说明理由．

如图，二次函数的图象过原点，与x轴的另一个交点为(8，0)．
（1）求该二次函数的解析式．
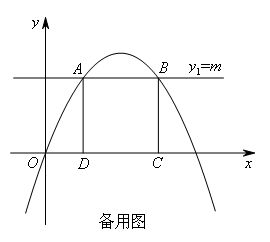
（2）在x轴上方作x轴的平行线y₁=m，交二次函数图象于A，B两点，过A，B两点分别作x轴的垂线，垂足分别为点D，点C．当矩形ABCD为正方形时，求m的值．
（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P，Q两点同时停止运动，设运动时间为t秒（t＞0）．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A，E，F，Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．

如图，直线与x轴、y轴分别交于点B，C，抛物线过B，C两点，且与x轴的另一个交点为点A，连接AC．
（1）求抛物线的解析式；
（2）在抛物线上是否存在点D（与点A不重合），使得S_△DBC=S_△ABC，若存在，求出点D的坐标；若不存在，请说明理由；
（3）有宽度为2，长度足够长的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和点Q，交直线CB于点M和点N，在矩形平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．

如图，在平面直角坐标系中，已知抛物线y=ax²+bx+2（a≠0）与x轴交于A(-1，0)，B(3，0)两点，与y轴交于点C，连接BC．
（1）求该抛物线的解析式，并写出它的对称轴．
（2）已知F(1，1)，若E(x，y)是抛物线上一个动点（其中1<x<2），连接CE，CF，EF，求△CEF面积的最大值及此时点E的坐标．
（3）若点N为抛物线对称轴上一点，抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标，若不存在，请说明理由．

如图，抛物线y=ax²+bx+2与直线y=-x交第二象限于点E，与x轴交于A(-3，0)，B两点，与y轴交于点C，EC∥x轴．
（1）求抛物线的解析式；
（2）点P是直线y=-x上方抛物线上的一个动点，过点P作x轴的垂线交直线于点G，作PH⊥EO，垂足为H．设PH的长为，点P的横坐标为m，求与m的函数关系式（不必写出m的取值范围），并求出的最大值；
（3）如果点N是抛物线对称轴上的一个动点，抛物线上存在一动点M，若以M，A，C，N为顶点的四边形是平行四边形，请直接写出所有满足条件的点M的坐标．

如图1，若直线l：y=-2x+4交x轴于点A，交y轴于点B，将△AOB绕点O逆时针旋转90°得到△COD．过点A，B，D的抛物线h：y=ax²+bx+4．
（1）求抛物线h的表达式；
（2）若与y轴平行的直线m以1秒钟一个单位长度的速度从y轴向左平移，交线段CD于点M，交抛物线h于点N，求线段MN的最大值；
（3）如图2，点E为抛物线h的顶点，点P是抛物线h在第二象限上的一动点（不与点D，B重合），连接PE，以PE为边作图示一侧的正方形PEFG，随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．