（2021镇江）如图1，正方形ABCD的边长为4，点P在边BC上，⊙O经过A，B，P三点．
（1）若BP=3，判断边CD所在直线与⊙O的位置关系，并说明理由；
（2）如图2，E是CD的中点，⊙O交射线AE于点Q，当AP平分∠EAB时，求tan∠EAP的值．

（2021荆州）在矩形ABCD中，AB=2，AD=4，F是对角线AC上不与点A，C重合的一点，过F作FE⊥AD于E，将△AEF沿EF翻折得到△GEF，点G在射线AD上，连接CG．
（1）如图1，若点A的对称点G落在AD上，∠FGC=90°，延长GF交AB于H，连接CH．
①求证：△CDG∽△GAH；
②求tan∠GHC．
（2）如图2，若点A的对称点G落在AD延长线上，∠GCF=90°，判断△GCF与△AEF是否全等，并说明理由．

阅读下列材料：
题目：如图1，在△ABC中，已知∠A（∠A<45°），∠C=90°，AB=1，请用sinA，cosA表示sin2A．
解：如图2，作AB边上的中线CE，CD⊥AB于D，
则CE=AB=，∠CED=2∠A，CD=ACsinA，AC=ABcosA=cosA
在Rt△CED中，sin2A=sin∠CED==2ACsinA=2cosAsinA
根据以上阅读，请解决下列问题：
（1）如图3，在△ABC中，∠C=90°，BC=1，AB=3，求sinA，sin2A的值；
（2）上面阅读材料中，题目条件不变，请用sinA或cosA表示cos2A．

阅读理解：
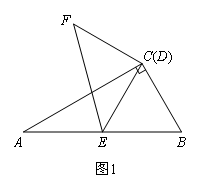
如图1，Rt△ABC中，a，b，c分别是∠A，∠B，∠C的对边，∠C=90°，其外接圆半径为R．根据锐角三角函数的定义：，，可得，
即（规定sin90°=1）．
（1）探究活动：
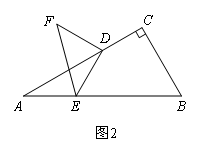
如图2，在锐角△ABC中，a，b，c分别是∠A，∠B，∠C的对边，其外接圆半径为R，那么：            （用＞，=或<连接），并说明理由．
事实上，以上结论适用于任意三角形．
（2）初步应用：
在△ABC中，a，b，c分别是∠A，∠B，∠C的对边，∠A=60°，∠B=45°，a=8，求b．
（3）综合应用：
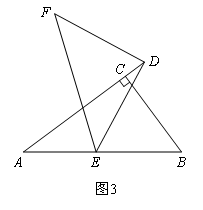
如图3，在某次数学活动中，小凤同学测量一古塔CD的高度，在A处用测角仪测得塔顶C的仰角为15°，又沿古塔的方向前行了100 m到达B处，此时A，B，D三点在一条直线上，在B处测得塔顶C的仰角为45°，求古塔CD的高度．（结果保留小数点后一位，≈1.732，）

如图，在□ABCD中，过点A作AE⊥DC于点E，连接BE，F为BE上一点，且∠AFE=∠D．
（1）求证：△ABF∽△BEC；
（2）若AD=5，AB=8，，求AF的长．

如图，在Rt△ACB中，∠ACB=90°，以点A为圆心，AC长为半径的圆交AB于点D，BA的延长线交⊙A于点E，连接CE，CD，F是⊙A上一点，点F与点C位于BE两侧，且∠FAB=∠ABC，连接BF．
（1）求证：∠BCD=∠BEC；
（2）若BC=2，BD=1，求CE的长及sin∠ABF的值．

如图，已知等腰直角三角形ABC中，D，E，F分别为边AB，AC，BC的中点，点M为斜边BC所在直线上一动点，且三角形DMN为等腰直角三角形（DM=DN，D，M，N呈逆时针）．
（1）如图1点M在边BC上，判断MF和AN的数量和位置关系，请直接写出你的结论．
（2）如图2点M在B点左侧时；如图3，点M在C点右侧．其他条件不变，（1）中结论是否仍然成立，并选择图2或图3的一种情况来说明理由．
（3）在图2中若∠DMB=α，连接EN，请猜测MF与EN的数量关系，即MF=        EN．（用含α的三角函数的式子表示）

通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比叫做顶角正对（sad），如图1，在△ABC中，AB=AC，顶角A的正对记作sadA，容易知道一个角的大小与这个角的正对值也是相互唯一确定的．根据上述角的正对定义，解下列问题：
（1）sad 60°=      ；
（2）对于0°<A<180°，∠A的正对值sadA的取值范围是        ；
（3）如图2，已知，其中∠A为锐角，试求sadA的值．

观察猜想
（1）如图1，在Rt△ABC中，∠ACB=90°，∠BAC=30°，点D与点C重合，点E在斜边AB上，连接DE，且DE=AE，将线段DE绕点D顺时针旋转90°得到线段DF，连接EF，则      ，sin∠ADE=      ；
探究证明
（2）在（1）中，如果将点D沿CA方向移动，使CD=AC，其余条件不变，如图2，上述结论是否保持不变？若改变，请求出具体数值：若不变，请说明理由；
（3）如图3，在△ABC中，∠ACB=90°，∠CAB=α，点D在边AC的延长线上，E是AB上任意一点，连接DE．ED=nAE，将线段DE绕着点D顺时针旋转90°至点F，连接EF．求和sin∠ADE的值分别是多少？（请用含有n，α的式子表示）