已知：如图，在四边形ABCD中，∠ADC=90°，连接AC，∠ACD=45°，AE平分∠CAD．
求证：DE=AC-AD．

先在图上走通思路后再填写空格内容：
①要证明DE=AC-AD，是线段的和差倍分，考虑         ，这里采用截长；
②结合条件AE平分∠CAD，考虑                     （辅助线），然后证全等，理由是       ，由全等的性质得         ，为接下来的全等准备条件；
③由已证的全等和条件∠ADC=90°，∠ACD=45°，得        ，等量代换DE=FC，从而得AC=AD+DE，即DE=AC-AD．
以上空缺处依次所填最恰当的是(    )

已知，如图，在五边形ABCDE中，AB=AE，∠BAE=2∠CAD，∠ABC+∠AED=180°，
求证：BC+DE=CD．

（补短法）证明：如图，                        

                        
在△ABC和△AEF中

∴△ABC≌△AEF（SAS）
∴∠2=∠3，AC=AF
                        
在△CAD和△FAD中

∴△CAD≌△FAD（SAS）
                        
请你仔细观察下列序号所代表的内容：
①延长DE到F，使EF=BC，连接AF；②延长DE到F，使BC=EF；
③延长DE到F，连接AF；④；
⑤；⑥；⑦；
⑧；⑨．
以上空缺处依次所填最恰当的是(    )

已知，如图，在五边形ABCDE中，AB=AE，AD平分∠CDE，∠BAE=2∠CAD，
求证：BC+DE=CD．

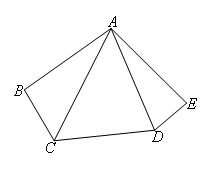
（截长法）证明：如图，                        

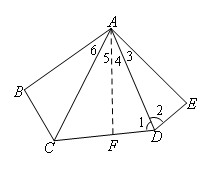
∵AD平分∠CDE
∴∠1=∠2
在△AFD和△AED中

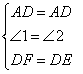
∴△AFD≌△AED（SAS）
∴                        
                        
在△ABC和△AFC中

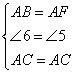
∴△ABC≌△AFC（SAS）
∴BC=CF
∴BC+DE=CF+DF
       =CD
请你仔细观察下列序号所代表的内容：
①在CD上截取CF=CB，连接AF；②在DC上截取DF=DE，连接AF；
③在DC上截取DF=DE；④AE=AF；⑤AF=AE，∠4=∠3；⑥∠4=∠3；
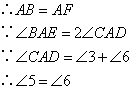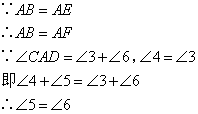⑦；⑧；⑨．
以上空缺处依次所填最恰当的是(    )

已知，如图，BM平分∠ABC，点P为BM上一点，PD⊥BC于点D，BD=AB+DC．
求证：∠BAP+∠BCP=180°．

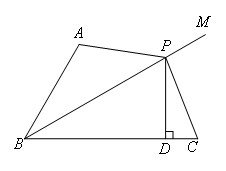
（补短法）证明：如图，                           

                           
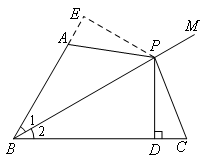
∵BP平分∠ABC
∴∠1=∠2
在△BEP和△BDP中

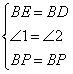
∴△BEP≌△BDP（SAS）
                           
在△PEA和△PDC中

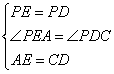
∴△PEA≌△PDC（SAS）
∴∠C=∠PAE
∵∠BAP+∠PAE=180°
∴∠BAP+∠BCP=180°
请你仔细观察下列序号所代表的内容：
①延长BA，过点P作PE⊥BA于点E；②延长BA到E，使AE=DC，连接PE；
③延长BA到E，使DC=AE；④；⑤；
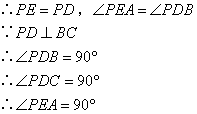⑥；⑦．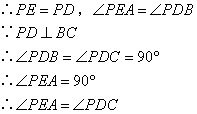
以上空缺处依次所填最恰当的是(    )

已知，如图，BM平分∠ABC，P为BM上一点，PD⊥BC于点D，BD=AB+CD．
求证：∠BAP+∠BCP=180°．

（截长法）证明：如图，在BC上截取BE=BA，连接PE．

                           
在△ABP和△EBP中

∴△ABP≌△EBP（SAS）
∴                           
                           
∴CD=ED
∵PD⊥BC
∴PE=PC
                           
请你仔细观察下列序号所代表的内容：
①；②∵∠1=∠2；③∠A=∠BEP；④AP=PE；
⑤；⑥；⑦；
⑧．
以上空缺处依次所填最恰当的是(    )

如图，已知AC平分∠DAB，CE⊥AB于点E，AB=AD+2BE，则下列结论：①；②∠ADC+∠B=180°；③CD=CB；④．其中正确结论的个数是(    )

已知：如图，在四边形ABCD中，AD=AB，∠ABC=∠ADC=∠BAD=90°，∠1=∠2．
求证：AE=BE+DF．

证明：如图，延长CB到点G，使BG=DF，连接AG．

                           
在△ABG和△ADF中

∴△ABG≌△ADF（SAS）
∴                           
∵∠BAD=90°
∴∠GAF=90°
∴∠GAE=90°-∠1
                           
∵∠1=∠2
∴∠GAE=∠G
∴AE=GE
    =BE+GB
    =BE+DF
请你仔细观察下列序号所代表的内容：
①；②；③∠3=∠2，AG=AF；④∠3=∠2，∠G=∠4；

⑤；⑥．
以上空缺处依次所填最恰当的是(    )

如图，已知AC平分∠DAB，CE⊥AB于点E，AB=AD+2BE，则下列结论不一定正确的是(    )

如图，已知AB=CD=AE=BC+DE=2，∠ABC=∠AED=90°，则五边形ABCDE的面积为(    )

已知：如图，在四边形ABCD中，AB=AD，∠ADC=∠B=∠BAD=90°，点E在BC的延长线上，点F在CD的延长线上，EAF=45°．
求证：DF=BE-EF．

先在图上走通思路后再填写空格内容：
①要证明DF=BE-EF，是线段的和差倍分，考虑         ，解决本题用的是     ；
②结合条件AB=AD，∠ADC=∠B=90°，考虑                              （辅助线），然后证全等，理由是       ，由全等的性质得         ，为接下来的全等准备条件；
③由已证的全等和条件∠BAD=90°，∠EAF=45°，得        ，然后证全等，理由是       ，由全等的性质得         ，从而得DF=BE-EF．
以上空缺处依次所填最恰当的是(    )