1编号:139455题型:解答题测试正确率:0%
2编号:139454题型:解答题测试正确率:0%
3编号:139451题型:解答题测试正确率:0%
4编号:139447题型:填空题测试正确率:0%
5编号:139334题型:解答题测试正确率:0%
6编号:139332题型:解答题测试正确率:0%
7编号:138059题型:解答题测试正确率:0%
(2021广安)如图,在平面直角坐标系中,抛物线y=-x2+bx+c的图象与坐标轴相交于A,B,C三点,其中点A的坐标为(3,0),点B的坐标为(-1,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒![]() 个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
个单位长度的速度向点C做匀速运动;同时,动点Q从点B出发,在线段BA上以每秒1个单位长度的速度向点A做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接PQ,设运动时间为t秒.
(1)求b,c的值.
(2)在P,Q运动的过程中,当t为何值时,四边形BCPQ的面积最小,最小值为多少?
(3)在线段AC上方的抛物线上是否存在点M,使△MPQ是以点P为直角顶点的等腰直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.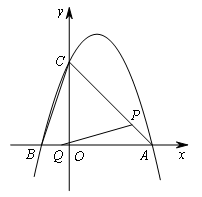
8编号:138055题型:解答题测试正确率:0%
9编号:128331题型:解答题测试正确率:0%
10编号:128329题型:解答题测试正确率:0%