已知：如图，AB∥EF，∠E=∠CAE，∠DAB=65°．
求∠ACF的度数．

解：如图，
∵AB∥EF（已知）
∴∠DAB=∠E（                       ）
∵∠DAB=65°，（已知）
∴∠E=65°（等量代换）
∵∠E=∠CAE（已知）
∴∠CAE=65°（                       ）
∵∠ACF是△ACE的一个外角（外角的定义）
∴∠ACF=∠E+∠CAE    
       =65°+65°    
       =130°（                       ）
①两直线平行，同位角相等；②同位角相等，两直线平行；③等量代换；④等式的性质；⑤三角形的一个外角等于和它不相邻的两个内角的和；⑥三角形的内角和是180°．
以上空缺处依次所填正确的是(    )

已知：如图，AB∥CD，∠EBA=60°，∠D=50°，求∠E的度数．

解：如图，
∵AB∥CD（已知）
∴∠EBA=∠EFC（两直线平行，同位角相等）
∵∠EBA=60°（已知）
∴∠EFC=60°（等量代换）
∵∠EFC是△EDF的一个外角（外角的定义）
∴∠EFC=∠D+∠E（                       ）
∵∠D=50°（已知）
∴∠E=∠EFC-∠D     
     =60°-50°      
     =10°（                       ）
①三角形的内角和是180°；②同角或等角的补角相等；③三角形的一个外角等于和它不相邻的两个内角的和；④等式的性质；⑤等量代换．
以上空缺处依次所填正确的是(    )

如图，直线∥，若∠1=150°，∠2=70°，则∠3的度数为(    )

已知：如图，在△ABC中，CD平分∠ACB，DE∥AC，EF∥CD．
求证：∠1=∠2．

证明：如图，

∵CD平分∠ACB（已知）
∴∠3=∠4（角平分线的定义）
∵DE∥AC（已知）
∴∠3=      （两直线平行，内错角相等）
∴∠4=∠5（等量代换）
∵EF∥CD（已知）
∴∠1=      （两直线平行，同位角相等）
∠5=      （两直线平行，内错角相等）
∴∠1=∠2（等量代换）
①∠1；②∠2；③∠3；④∠4；⑤∠5．
以上空缺处依次所填正确的是（    ）

已知：如图，在△ABC中，D为BC边上一点，DF⊥AB于F，DE∥AC，∠A=∠B．
求证：∠1=∠2．

证明：如图，
∵DE∥AC（已知）
∴∠A＝      （两直线平行，同位角相等）
∵∠A=∠B（已知）
∴∠B＝∠FED（等量代换）
∵DF⊥AB（已知）
∴∠FED+∠1=90°，
∠B+∠2=90°（                    ）
∴∠1=∠2（                    ）
①∠1；②∠FED；③直角三角形两锐角互余；④垂直的性质；⑤同角或等角的补角相等；
⑥同角或等角的余角相等；⑦等量代换．
以上空缺处依次所填正确的是(    )

已知：如图，△ABC．D为BC上任意一点，过点D作DE∥AB交AC于点E，作DF∥AC交AB于点F．
求证：∠A+∠B+∠C=180°．

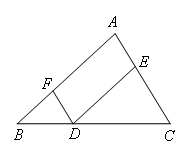
证明：如图，

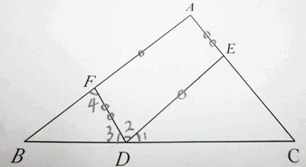
∵DE∥AB（辅助线的作法）
∴∠1＝∠B（两直线平行，同位角相等）
∠2＝∠4（                    ）
∵DF∥AC（辅助线的作法）
∴∠3＝      ，∠A＝∠4（两直线平行，同位角相等）
∴∠2＝∠A（等量代换）
∵∠1+∠2+∠3=180°（                    ）
∴∠A+∠B+∠C=180°（等量代换）
①两直线平行，内错角相等；②两直线平行，同位角相等；③内错角相等，两直线平行；④∠DEA；
⑤∠DEC；⑥∠C；⑦平角的定义；⑧三角形的内角和是180°．
以上空缺处依次所填正确的是(    )

如图，AB∥CD，EF交AB于点G，交CD于点H，HP平分∠GHD，交AB于点P，∠AGE=50°，求∠PHD的度数．

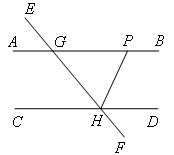
解：如图，
∵AB∥CD（已知）
∴∠GHC=∠AGE（                  ）
∵∠AGE=50°（已知）
∴∠GHC=50°（等量代换）
∴∠GHD=180°-50°=130°（                  ）
∵HP平分∠GHD（已知）
∴∠PHD=∠GHD=×130°=65°（角平分线的定义）
①平角的定义；②等量代换；③内错角相等，两直线平行；④同位角相等，两直线平行；
⑤同旁内角互补，两直线平行；⑥两直线平行，内错角相等；⑦两直线平行，同位角相等；
⑧等式的性质．
以上空缺处依次所填正确的是(    )

如图，AB∥CD，∠α=60°，∠C=∠D，求∠B的度数．
推理过程如下：

解：如图，
∵AB∥CD（已知）
∴∠α=∠D（两直线平行，同位角相等）
∠B+      =180°（两直线平行，同旁内角互补）
∵∠C=∠D（已知）
∴∠C=∠α（                  ）
∵∠α=60°（已知）
∴∠C=60°（等量代换）
∴∠B=180°-∠C       
     =180°-60°      
     =120°（                  ）
①∠D；②∠DAB；③∠C；④等量代换；⑤等式的性质．
以上空缺处依次所填正确的是(    )

已知：如图，AB∥CD，EF分别交AB，CD点于M，N，∠EMB=40°，MG平分∠BMN交CD于点G．求∠1的度数．

解：如图，
∵∠EMB=40°（已知）
∴∠BMN=180°-∠EMB
=180°-40°
=140°（                  ）
∵MG平分∠BMN（已知）

∵AB∥CD（已知）
∴∠1=∠BMG（两直线平行，内错角相等）
∴∠1=70°（                  ）
①平角的定义；②等式的性质；③等量代换；④两直线平行，内错角相等；
⑤两直线平行，同位角相等；⑥两直线平行，同旁内角互补．
以上空缺处依次所填正确的是(    )

已知：如图，AB∥CD，∠1+∠C=180°．
求证：AD∥BC．

证明：如图，

∵AB∥CD（已知）
∴∠1=      （两直线平行，内错角相等）
∵∠1+∠C=180°（已知）
∴∠2+      =180°（等量代换）
∴AD∥BC（同旁内角互补，两直线平行）
①∠D；②∠2；③∠C；④∠FDE；⑤∠DAB．
以上空缺处依次所填正确的是(    )