2010河南（1）操作发现如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．（2）问题解决保持（1）中的条件不变，若DC=2DF，求的值；（3）类比探求保持（1）中条件不变，若DC=nDF，求的值．

(2011河北)如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是　　　　　　　　　　　　.

（2011•甘肃兰州）如图，依次连结第一个矩形各边的中点得到一个菱形，再依次连结菱形各边的中点得到第二个矩形，按照此方法继续下去，已知第一个矩形的面积为1，则第n个矩形的面积为()

（2011•四川省内江市） 在直角坐标系中，正方形A₁B₁C₁O，A₂B₂C₂C₁、…、A_nB_nC_nC_n-1按如图所示的方式放置，其中点A₁、A₂、A₃、…、A_n均在一次函数y=kx+b的图象上，点B₁、B₂、B₃、…、B_n均在x轴上．若点B₁的坐标为（1，1），点B₂的坐标为（3，2），则点A_n的坐标为()

(2011浙江中考)如图下面是按照一定规律画出的一行“树形图”，经观察可以发现：图A₂比图A₁多出了2个“树枝”，图A₃比图A₂多出了4个“树枝”，图A₄比图A₃多出了8个“树枝”，…，照此规律，则图A₆比图A₂多出 “树枝”()

（2011山东菏泽）填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是（）

观察下列图形

根据图一、二、三的规律，图四中三角形的个数为________个.

意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…， 其中从第三个数起，每一个数都等于它前面两上数的和．现以这组数中的各个数作为正方形的长度构造如下正方形：

再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩形并记为①、②、③、④.相应矩形的周长如下表所示：


若按此规律继续作矩形，则序号为⑩的矩形周长是_______________.

（2011浙江）以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点，得四边形EFGH．
（1）如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；如图2，当四边形ABCD为矩形时，请判断：四边形EFGH的形状（不要求证明）；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=α（0°＜α＜90°），
① 试用含α的代数式表示∠HAE；
② 求证：HE=HG；
③ 四边形EFGH是什么四边形？并说明理由

（2011辽宁）在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠DOC=α.将△DOC绕点O按逆时针方向旋转得到△D’OC’（0°＜旋转角＜90°）.连接AC’、BD’，AC’与BD’相交于点M.
（1）当四边形ABCD是矩形时，如图1，请猜想AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想；
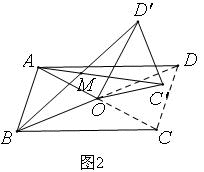
（2）当四边形ABCD是平行四边形时，如图2，已知AC=kBD，请猜想此时AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想；
（3）当四边形ABCD是等腰梯形时，如图3，AD∥BC，此时（1）中AC’与BD’的数量关系是否成立？∠AMB与α的大小关系是否成立？不必证明，直接写出结论.