如图，在Rt△ABC中，∠ACB=90°，∠B=30°，CD⊥AB于点D，∠DCE=15°，
∠CEF=135°．求证：EF∥BC．

证明：如图，
∵CD⊥AB（已知）
∴∠CDB=90°（垂直的性质）
∵∠B=30°（已知）
∴∠DCB=90°-∠B=60°（直角三角形两锐角互余）
                       
∴EF∥BC（同旁内角互补，两直线平行）
横线处应填写的过程最恰当的是(    )

已知：如图，在△ABC中，∠BAC=50°，∠ABC=60°，AD⊥BC，BE⊥AC，垂足分别为D，E，AD，BE相交于点H，求∠AHB的度数．

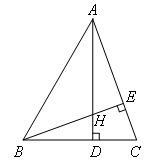
解：如图，

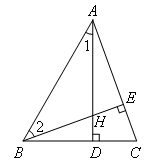
∵AD⊥BC（已知）
∴∠ADB=90°（垂直的性质）
∵∠ABC=60°（已知）
∴∠1=90°-∠ABC
     =90°-60°
     =30°（直角三角形两锐角互余）
∵BE⊥AC（已知）
∴                    
∵∠BAC=50°（已知）
∴                    
∴                    
横线处应填写的过程依次正确的是(    )
①∠BEA=90°（垂直的性质）
②∠ADB=90°（垂直的性质）
③∠BAC=50°（已知）
④∠2=90°-∠BAC=90°-50°=40°（直角三角形两锐角互余）
⑤∠2=50°（直角三角形两锐角互余）
⑥∠AHB=180°-∠1-∠2=180°-30°-40°=110°（三角形的内角和等于180°）
⑦∠AHB=90°+∠1=90°+30°=120°（三角形的一个外角等于和它不相邻的两个内角的和）

已知：如图，在△ABC中，AD平分∠BAC，E为AD上一点，且EF⊥BC于点F．
若∠C=35°，∠DEF=15°，则∠B的度数为(    )

如图，在△ABC中，AD⊥BC于点D，E是AC边上一点，BE与AD交于点F．∠ABC=45°，
∠BAC=75°，∠BFA=120°，则∠BEC的度数是(    )

如图，将Rt△ABC的直角顶点C放在直线a上，∠ACB=90°，a∥b，∠1=50°，
∠A=60°，则∠2的度数为(    )

如图，点C在AB的延长线上，CE⊥AF于点E，交BF于点D．若∠F=40°，∠C=20°，
则∠FBC的度数为(    )

如图，在Rt△ABC中，∠ACB=90°，，沿△ABC的中线OC将△AOC折叠，使点A落在点D处．若CD⊥AB于点M，则tanA的值为(    )

已知：如图，在△ABC中，∠ACB=90°，E是BC边上的一点，过C作CF⊥AE于点F，过B作BD⊥BC于点B，交CF的延长线于点D．若∠EAC=25°，求∠D的度数．

解：如图，

∵CF⊥AE（已知）
∴∠EAC+∠2=90°（直角三角形两锐角互余）
∵∠ACB=90°
即∠1+∠2=90°（已知）
                   
∴∠1=25°（等量代换）
∵BD⊥BC（已知）
∴∠DBC=90°（垂直的性质）
∴∠D+∠1=90°（直角三角形两锐角互余）
∴∠D=90°-∠1
     =90°-25°
     =65°（等式性质）
横线处应填写的过程最恰当的是(    )

如图，在△ABC中，点D在BC的延长线上，过点D作DE⊥AB于点E，交AC于点F．已知∠A=35°，∠FCD=85°，求∠D的度数．

解：如图，
∵∠FCD是△ABC的一个外角（外角的定义）
∴∠FCD=∠A+∠B（三角形的一个外角等于和它不相邻的两个内角的和）
                                
∵DE⊥AB（已知）
∴∠BED=90°（垂直的性质）
∴∠D=90°-∠B
     =90°-50°
     =40°（直角三角形两锐角互余）
横线处应填写的过程最恰当的是(    )

已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．
求证：AB∥DG．

证明：如图，

∵EF⊥BC（已知）
∴∠EFB=90°（垂直的性质）
∴∠B+∠1=90°（                    ）
∵AD⊥BC（已知）
∴∠2+∠3=90°（垂直的性质）
∵∠1=∠2（已知）
∴∠B=∠3（                    ）
∴            （同位角相等，两直线平行）
①垂直的性质；②直角三角形两锐角互余；③同角或等角的余角相等；④同角或等角的补角相等；
⑤等量代换；⑥EF∥AD；⑦AB∥DG．
以上空缺处依次所填正确的是(    )