1编号:139546题型:解答题测试正确率:0%
2编号:139545题型:解答题测试正确率:0%
3编号:139379题型:解答题测试正确率:0%
阅读与思考:利用多项式的乘法法则可推导得出:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.因式分解与整式乘法是方向相反的变形,利用这种关系可得:x2+(p+q)x+pq=(x+p)(x+q).利用这个式子可以将某些二次项系数为1的二次三项式分解因式,例如:将式子x2+3x+2分解因式.分析:这个式子的常数项2=1×2,一次项系数3=1+2.这是一个x2+(p+q)x+pq型的式子,∴x2+3x+2=x2+(1+2)x+1×2,
∴x2+3x+2=(x+1)(x+2).
(1)填空:
式子x2+7x+10的常数项10= × ,一次项系数7= + ,分解因式x2+7x+10= .
(2)若x2+px+8可分解为两个一次因式的积,请直接写出整数p的所有可能值.
4编号:139041题型:解答题测试正确率:0%
定义:对于一个两位数x,如果x满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“相异数”,将一个“相异数”的个位数字与十位数字对调后得到一个新的两位数,将这个新两位数与原两位数的求和,同除以11所得的商记为S(x).如a=13的个位数字与十位数字对调后的新两位数为31,新两位数与原两位数的和为13+31=44,和44除以11的商为44÷11=4,所以S(13)=4.
(1)计算:S(43)= .
(2)若一个“相异数”y的十位数字是k,个位数字是2(k-1),且S(y)=10,求相异数y.
(3)小慧同学发现若S(x)=5,则“相异数”x的个位数字与十位数字之和一定为5,请判断小慧的发现是否正确?如果正确,说明理由;如果不正确,举出反例.
5编号:138614题型:解答题测试正确率:0%
6编号:138102题型:解答题测试正确率:0%
(2020鄂尔多斯)我们知道,顶点坐标为(h,k)的抛物线的解析式为y=a(x-h)2+k(a≠0).今后我们还会学到,圆心坐标为(a,b),半径为r的圆的方程(x-a)2+(y-b)2=r2,如:圆心为点P(-2,1),半径为3的圆的方程为(x+2)2+(y-1)2=9.
(1)以点M(-3,-1)为圆心,![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)如图,以点B(-3,0)为圆心的圆与y轴相切于原点,点C是⊙B上一点,连接OC,作BD⊥OC,垂足为点D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,求证:EC是⊙B的切线;
②在BE上是否存在一点Q,使QB=QC=QE=QO?若存在,求点Q的坐标,并写出以点Q为圆心,以QB为半径的⊙Q的方程;若不存在,请说明理由.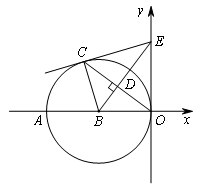
7编号:137783题型:解答题测试正确率:0%
8编号:137759题型:解答题测试正确率:0%
9编号:137691题型:解答题测试正确率:0%
10编号:137646题型:解答题测试正确率:0%