如果关于x的方程kx²-(2k+1)x+(k+2)=0有实数根，求k的取值范围.

孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点，两直角边与该抛物线交于、两点，请解答以下问题：
（1）若测得OA=OB=（如图1），求a的值；
（2）对同一条抛物线，孔明将三角板绕点O旋转到如图2所示位置时，过B作BF⊥x轴于点F，测得OF=1，写出此时点B的坐标，并求点A的横坐标；
（3）对该抛物线，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B的连线段总经过一个固定的点，试说明理由并求出该点的坐标．

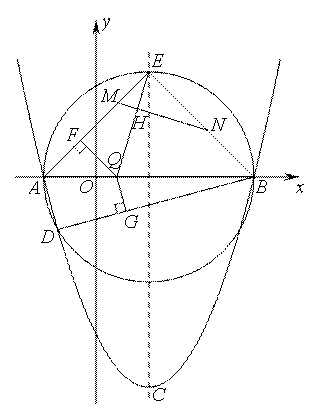
已知抛物线y=ax²+bx+c(a＜0)，顶点C的坐标为（1，-4），且与x轴交于A、B两点，A（-1，0）．
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于E，依次连接A、D、B、E，点Q为AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断是否为定值，若是，请求出此定值，若不是，请说明理由；
（3）在（2）的条件下，若点H是线段EQ上一点，过点H作MN⊥EQ，MN分别与边AE、BE相交于M、N（M与A、E不重合，N与E、B不重合），请判断是否成立，若成立，请给出证明，若不成立，请说明理由．

如图，Rt△ABC中，AB=8，BC=6，Rt△DBE中，DB=5，BE=7，将两直角三角形直角顶点以及两直角边按如图方式重叠在一起，两斜边交于点P，求点P到AB边的距离是多少？

已知，如图，在△ODC中，∠D=90°，EC是∠DCO的角平分线，且OE⊥CE，过点E做EF⊥OC交OC于点F，猜想：线段EF与OD之间的数量关系，并加以证明.

（2011湖南常德）如图，已知四边形ABCD是平行四边形.若AF、BE分别是∠DAB、∠CBA的平分线，求证：DF=EC.

如图，△ABC中，BC=18，若BD⊥AC于D，CE⊥AB于E，F、G分别为BC、DE的中点，若ED=10，求FG的长．

如图，在矩形OABC中，点O为原点，点A的坐标为(0，8)，点C的坐标为(6，0)．抛物线经过点A、C，与AB交于点D．
（1）求抛物线的函数解析式；
（2）点P为线段BC上一个动点(不与点C重合)，点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．
①求S关于m的函数表达式；
②当S最大时，在抛物线的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

在平面直角坐标系xOy中，二次函数y=mx²+(m-3)x-3(m>0)的图象与x轴交于A、B两点（点A在点B左侧），与y轴交于点C.
（1）求点A的坐标；                                                            
（2）当∠ABC=45°时，求m的值；  
（3）已知一次函数y=kx+b，点P（n，0）是x轴上的一个动点，在（2）的条件下，过点P垂直于x轴的直线交这个一次函数的图象于点M，交二次函数y=mx²+(m-3)x-3(m>0)的图象于点N.若只有当-2<n<2时，点M位于点N的上方，求这个一次函数的解析式.

如图，在△ABC中，AD是BC边上的中线，分别以AB边、AC边为直角边各向外作等腰直角三角形，求证：EF=2AD.