1编号:29892题型:单选题测试正确率:41.27%
如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.
(3)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图3,其他条件不变,则(1)中得到的结论(MD⊥MF)是否发生变化?写出你的猜想并加以证明.
解题思路:(2)小明类比前两问,看到图3中M是AE的中点,并且AD∥BE,考虑延长DM交BE于点H,连接FD、FH,如下图,先证明 ,由全等的性质可以得到 .因为DC=AD,所以DC=HE,结合题目中的条件FC=FE,∠DCF=∠FEH==45°.又可以利用判定定理 证得 ,得到FD=FH,在等腰△DFH中,由等腰三角形三线合一,得到MF⊥DH,从而证明结论.
以上横线处,依次所填正确的是( )
①△ADM≌△EHM;②△DCF≌△HEF;③DM=HM,AD=HE;④FD=FH;⑤SSA;⑥ASA;⑦SAS.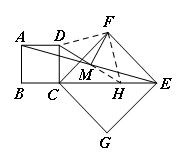
2编号:29891题型:单选题测试正确率:38.23%
如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.
(2)若将图1中的正方形CGEF绕点C顺时针旋转,使D,C,G三点在一条直线上,如图2,其他条件不变,则(1)中得到的结论(MD⊥MF)是否发生变化?写出你的猜想并加以证明.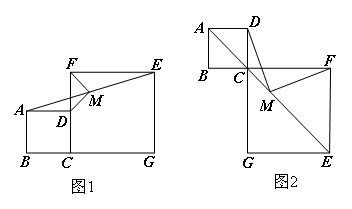
解题思路:(2)小明类比第(1)问,看到图2中M是AE的中点,并且AD∥GE,考虑延长DM交GE于点H,连接FD、FH.如下图,先证明 ,由全等的性质可以得到 ,进而可以得到DC=HE,由题目中的已知条件由∠DCF=∠FEH=90°,FC=FE,又可以利用判定定理 证得 ,得到FD=FH,在等腰△DFH中,由等腰三角形三线合一,得到 ,从而证明结论.
以上横线处,依次所填正确的是( )
①△ADM≌△EHM;②△FDC≌△FHE;③DM=HM,AD=HE;④FD=FH;⑤SSA;⑥ASA;⑦SAS;⑧MF⊥DH;⑨FM平分∠DFH.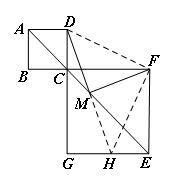
3编号:29890题型:单选题测试正确率:37.97%
如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.
(1)探究线段MD,MF的位置关系,并证明.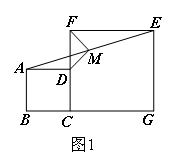
解题思路:(1)小明猜测MD⊥MF,看到图1中M是AE的中点,并且AD∥EF,考虑延长DM交EF于点H,如下图,先利用全等三角形的判定定理 ,证明 ,由全等的性质可以得到 ,所以CD=EH,进而可以得到FD=FH,在等腰△DFH中,由等腰三角形三线合一,得到 ,从而证明结论.
以上横线处,依次所填正确的是( )
①AAS;②ASA;③SAS;④△ADM≌△EHM;⑤△FDM≌△FHM;⑥DM=HM,AD=HE;⑦FD=FH;⑧MF⊥DH;⑨FM平分∠DFH.
4编号:29889题型:单选题测试正确率:33.67%
已知:如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于点E、F,图1、图2是旋转三角板所得图形的两种情况.
(2)若点E和点F分别在AB和BC边的延长线上时,如图2,OE=OF还成立吗?若成立,请给出证明,若不成立,请说明理由.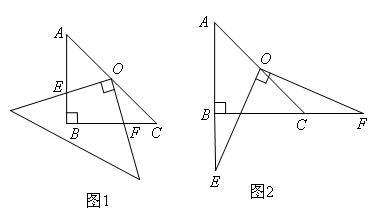
解题思路:(2)类比(1)的思路,添加的辅助线是 ,因为AB=BC,∠ABC=90°,所以△ABC是一个等腰直角三角形;根据点O是AC的中点,得到BO⊥AC,进而得到△BOC是等腰直角三角形,所以OB=OC,∠ACB=∠CBO=45°,又因为∠EOF=90°,根据 ,可以得到 ,又因为∠OBE=∠OCF=135°,根据全等三角形判定定理 ,可以得到 ,根据全等三角形的性质可以得到OE=OF.
①连接OB,②连接OB,使OB⊥AC,③∠BOE=∠FOC,④∠AOE=∠FCO,⑤同角的补角相等,⑥同角的余角相等,⑦△AOE≌△COF,⑧△BOE≌△COF,⑨AAS,⑩ASA,
以上横线处,依次所填正确的是( )
5编号:29888题型:单选题测试正确率:47.85%
已知:如图,在Rt△ABC中,AB=BC,∠ABC=90°.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于点E、F,图1、图2是旋转三角板所得图形的两种情况.
(1)若点E和点F分别在边AB和BC上,如图1,求证:OE=OF
解题思路:(1)连接OB,如下图,根据AB=BC,∠ABC=90°,可以得到∠C=45°,根据点O是AC的中点,得到BO⊥AC,BO平分∠ABC,∠ABO=45°=∠C,进而得到△BOC是等腰直角三角形,所以OB=OC,又因为∠EOF=90°,所以∠EOF=∠BOC=90°,根据 ,可以得到∠BOE=∠COF,根据全等三角形判定定理 ,可以得到 ,根据全等三角形的性质可以得到OE=OF.
①同角的补角相等,②同角的余角相等,③△AOE≌△COF,④△BOE≌△COF,⑤AAS,⑥ASA
以上横线处,依次所填正确的是( )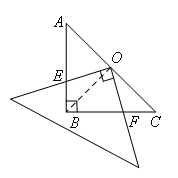
6编号:29887题型:单选题测试正确率:66.08%
7编号:29886题型:单选题测试正确率:47.34%
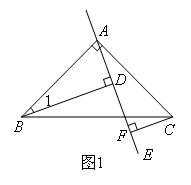
已知:如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C在AE的异侧,BD⊥AE于点D,CF⊥AE于点F.
(2)若直线AE绕A点旋转到如图2的位置时(BD<CF),其余条件不变,则BD与DF、CF的数量关系如何?请给予证明.
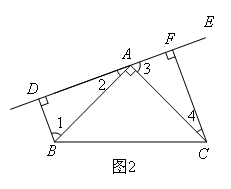
解题思路:(2)类比第(1)问,猜测DF=BD+CF.
∠BAC=90°,BD⊥AE,CF⊥AE,得到∠ADB=∠AFC=90°,所以∠2+∠1=90°,∠2+∠3=90°,得到 理由是 .
又因为AB=AC,∠BDA=∠AFC=90°,因此根据全等三角形判定定理 ,可以得到 ,由全等的性质得到CE=AF,BE=CF,最后得到DF=DA+AF=CF+BD.
①∠3=∠1;②∠1=∠4;③同角的余角相等;④同角的补角相等;⑤△ADB≌△AFC;⑥△ADB≌△CFA;⑦AAS;⑧ASA;
以上横线处,依次所填正确的是( )
8编号:29885题型:单选题测试正确率:58.23%
已知:如图1,△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C在AE的异侧,BD⊥AE于点D,CF⊥AE于点F.
(1)试证明BD=DF+CF.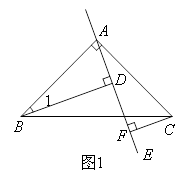
解题思路:(1)由∠BAC=90°,BD⊥AE,CF⊥AE,得到∠ADB=∠AFC=90°,所以∠BAD+∠1=90°,∠BAD+∠FAC=90°,得到 理由是 .又因为AB=AC,∠BDA=∠AFC=90°,因此根据全等三角形判定定理 ,可以得到 ,由全等的性质得到CE=AF,BE=CF,最后得到BD=AF=AD+DF=CF+DF.
①∠BAD=∠ACF;②∠FAC=∠1;③同角的余角相等;④同角的补角相等;⑤△ADB≌△AFC;⑥△ADB≌△CFA;⑦AAS;⑧ASA;
以上横线处,依次所填正确的是( )
9编号:29858题型:单选题测试正确率:83.51%
10编号:29857题型:单选题测试正确率:83.87%