1编号:136990题型:解答题测试正确率:0%
2编号:136973题型:解答题测试正确率:0%
3编号:136884题型:解答题测试正确率:0%
4编号:136712题型:解答题测试正确率:0%
5编号:136711题型:解答题测试正确率:0%
6编号:136707题型:解答题测试正确率:0%
7编号:136688题型:解答题测试正确率:0%
在△ABC中,AC=BC,CD是AB边上的高.
问题发现:
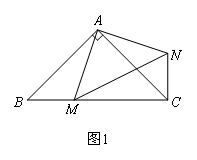
(1)如图1,若∠ACB=90°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转90°,得到线段CF,连接BF,我们会发现CD,BE,BF之间的数量关系是CD=![]() (BE+BF),请你证明这个结论;
(BE+BF),请你证明这个结论;
提出猜想:
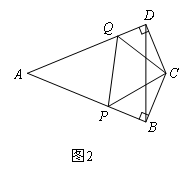
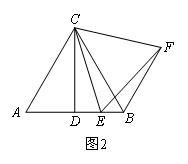
(2)如图2,若∠ACB=60°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转60°,得到线段CF,连接BF,猜想线段CD,BE,BF之间的数量关系是 ;
拓广探索:
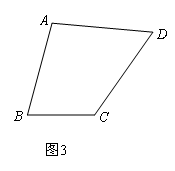
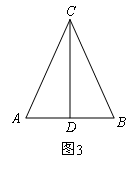
(3)若∠ACB=α,CD=k·AB(k为常数),点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转α,得到线段CF,连接BF.请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.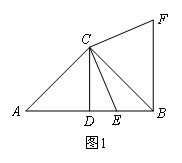
8编号:136683题型:解答题测试正确率:0%
9编号:135951题型:解答题测试正确率:0%
10编号:135414题型:解答题测试正确率:0%
(2021鄂尔多斯)旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)尝试解决:如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC,点M是BC上的一点,BM=1 cm,CM=2 cm,将△ABM绕点A旋转后得到△ACN,连接MN,则AM= cm;
(2)类比探究:如图2,在“筝形”四边形ABCD中,AB=AD=a,CB=CD,AB⊥BC于点B,AD⊥CD于点D,点P,Q分别是AB,AD上的点,且∠PCB+∠QCD=∠PCQ,求△APQ的周长;(结果用a表示)
(3)拓展应用:如图3,已知四边形ABCD,AD=CD,∠ADC=60°,∠ABC=75°,AB=![]() ,BC=2,求四边形ABCD的面积.
,BC=2,求四边形ABCD的面积.