已知：如图，在△ABC中，AB>AC，E为BC的中点，AD平分∠BAC，过E作EF∥AD，交AB于点G，交CA的延长线于点F，求证BG=CF．

如图，先在图上走通思路后再填写空格内容：

①因为点E是BC的中点，考虑延长GE到点H，使EH=GE，连接CH；
②进而利用全等三角形的判定         ，证明       ≌       ；
③由全等可得                ；
④再与已知条件重新组合，经过推理，可得BG=CF．
以上空缺处依次所填最恰当的是(    )

已知：如图，在四边形ABCD中，AD∥BC，E是CD的中点，若AB=AD+BC，∠ABC=50°，求∠BAE的度数．

如图，先在图上走通思路后再填写空格内容：

①因为AD∥BC，E是CD的中点，考虑                           （辅助线）；
②进而利用全等三角形的判定         ，证明       ≌       ；
③由全等可得                ；
④结合已知条件AB=AD+BC，得AB=BF，从而∠BAE=∠F，所以在△ABF中，根据三角形的内角和等于180°，得．
以上空缺处依次所填最恰当的是(    )

已知：如图，在四边形ABCD中，AD∥BC，E为AB的中点，G，F分别为AD，BC边上的点，且GE⊥EF．
求证：GF=AG+BF．

如图，先在图上走通思路后再填写空格内容：

①因为AD∥BC，E为AB的中点，考虑延长GE交FB的延长线于点H；
②进而利用全等三角形的判定         ，证明       ≌       ；
③由全等可得                ；
④结合已知条件，得EF垂直平分GH，根据线段垂直平分线上的点到这条线段两个端点的距离相等，可得                ，可得FG=AG+BF．
以上空缺处依次所填最恰当的是(    )

已知：如图，点E是BC的中点，∠BAE=∠D．
求证：AB=CD．

如图，先在图上走通思路后再填写空格内容：

①因为点E是BC的中点，考虑延长AE到点F，使EF=AE，连接CF；
②进而利用全等三角形的判定         ，证明       ≌       ；
③由全等可得                ；
④结合已知条件∠BAE=∠D，得∠F=∠D，在△DCF中，利用           ，可得CF=CD，等量代换得AB=CD．
以上空缺处依次所填最恰当的是(    )

已知：如图，在△ABC中，AD是BC边上的中线，分别以AB，AC为直角边向外作等腰直角三角形ABE和等腰直角三角形ACF，连接EF．某同学通过添加辅助线：延长AD到点M，使DM=AD，连接BM．则下列结论错误的是(    )

已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，
求证：∠C=∠BAE．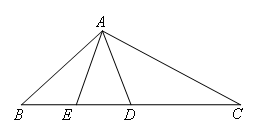

证明：如图，                            ．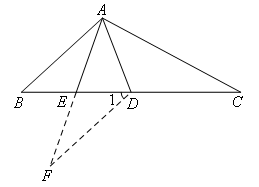

∵AE是△ABD的中线
∴BE=ED
在△ABE和△FDE中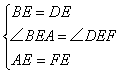

∴△ABE≌△FDE（SAS）
∴                            
∵CD=AB
∴CD=FD
∵∠ADF=∠ADB+∠1
∠ADB=∠BAD
∴∠ADF=∠BAD+∠B
∵在△ABD中，∠ADB=180°-（∠BAD+∠B）
∴∠ADC=180°-∠ADB
=180°-[180°-（∠BAD+∠B）]
=∠BAD+∠B
∴∠ADF=∠ADC
在△FAD和△CAD中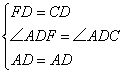

∴△FAD≌△CAD（SAS）
∴                            
∴∠C=∠BAE
请你仔细观察下列序号所代表的内容：
①延长AE到F，连接DF，使得DF∥AB；
②延长AE到F，使得EF=AE，连接DF；
③延长AE到F，使得EF=AE，连接DF，过D作DF∥AB；
④AB=FD，AE=EF；
⑤AB=FD，∠BAE=∠F，∠B=∠1；
⑥AB=FD；
⑦AF=AC；
⑧∠F=∠C．
以上空缺处依次所填最恰当的是(    )

已知，在△ABC中，AB=5，中线AD=7，则边AC的取值范围是(    )

已知：如图，在△ABC中，AD为BC边的中线，AD=5，AC=8，求边AB的取值范围．

解：如图，                            ．

∴AE=2AD
∵AD=5
∴AE=10
∵AD是BC边上的中线
∴BD=CD
在△CDE和△BDA中

∴△CDE≌△BDA（SAS）
∴                            
在△ACE中，AC=8，
∴10-8 ∴2 请你仔细观察下列序号所代表的内容：
①延长AD到点E，使DE=AD，连接CE；
②延长AD到点E，连接CE；
③延长AD到点E，使DE=AD，连接CE，过点E作CE∥AB；
④CE=BA，∠E=∠BAD；
⑤CE=BA．
以上空缺处依次所填最恰当的是(    )

如图所示，△ABC中，AB=3，AC=7，AD为△ABC的中线，求AD的取值范围．

先在图上走通思路后再填写空格内容：
1．因为AD为△ABC的中线，考虑                                （辅助线叙述）；
2．进而利用全等三角形的判定         ，证明       ≌       ；
3．由全等可得                ；
4．观察图形，2AD放在△       中，利用三角形的三边关系，可得2以上空缺处依次所填最恰当的是(    )

已知CD=AB，∠BDA=∠BAD，AE是△ABD的中线，
求证：∠C=∠BAE．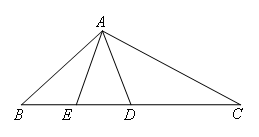

证明：如图，                            ．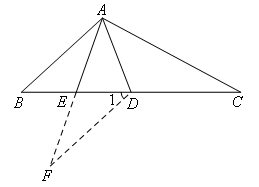

∵AE是△ABD的中线
∴BE=ED
在△ABE和△FDE中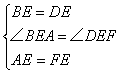

∴△ABE≌△FDE（SAS）
∴                            
∵CD=AB
∴CD=FD
∵∠ADF=∠ADB+∠1
∴∠ADF=∠ADB+∠B
∵∠ADC为△ABD的一个外角
∴∠ADC=∠B+∠BAD
∵∠ADB=∠BAD
∴∠ADF=∠ADC
在△FAD和△CAD中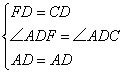

∴△FAD≌△CAD（SAS）
∴                            
∴∠C=∠BAE
请你仔细观察下列序号所代表的内容：
①延长AE到F，连接DF，使得DF∥AB；
②延长AE到F，使得EF=AE，连接DF；
③延长AE到F，使得EF=AE，连接DF，过D作DF∥AB；
④AB=FD，AE=EF；
⑤AB=FD，∠BAE=∠F，∠B=∠1；
⑥AB=FD；
⑦AF=AC；
⑧∠F=∠C．
以上空缺处依次所填最恰当的是(    )